“If you ever hear yourself saying, ‘I think I understand this,’ that means you don’t.” — Richard Feynman

Nothing about AI or machine learning is intuitive. Maybe that’s the point. 

An example is the sudden rise in popularity of something called “bfloat16,” a new way of representing numbers that holds magical appeal to AI/ML programmers – and, therefore for chipmakers as well. So, let’s look at bfloat16 for beginners. If you’re an experienced programmer, skip ahead. 

Binary Basics

To begin at the beginning, all computers represent numbers in binary format. That is, they don’t have ten fingers and toes to count on; they just have wires. A wire can carry electrical current or not, and we tend to think of it as being either on or off. Other times we might call it active or passive, high or low, energized or deenergized, true or false, 0 or 1. We could just as easily label these two conditions up and down, left and right, blue and green, charm and strange; it doesn’t matter. The point is that everything inside the machine boils down to those two alternatives. 

Counting with just two numbers, 0 and 1, might be a real hindrance, but, fortunately for us, people figured a way around this more than a century ago. It’s called binary notation (from the Latin word for two) and it works fine once you get over the initial weirdness of not being able to use the numbers 2 through 9.  

If you write down just one digit, you have a grand total of two options: 0 or 1. We call that a 1-bit number. If you write two digits, you have four options: 00, 01, 10, and 11. We call that a two-bit number. See where this is going? Three bits gives you eight different combinations, four bits yields sixteen, and so on. Every bit you add doubles the number of unique combinations you can write using those two numbers. 

We can treat these just like our normal everyday numbers but written in a different way, almost like a second language. For example, the pattern 0000 is zero. Easy enough. The pattern 0001 is the number one, 0010 is two, 0011 is three, 0100 is four, and so on, up to 1111, which is the number fifteen. So, with sixteen total possibilities, we’ve figured out how to write the numbers from zero to fifteen. 

What if you need numbers bigger than that, like, say, 186? Keep adding bits until you’ve got enough of them to write a bigger number. Remember, each bit doubles the largest value you can create. Q: How many bits would it take to write the binary version of 186? A: Eight bits, and you’d write it as 10111010. To your computer, your phone, and your thermostat, that’s the number 186.

Whatever Floats Your Numerical Boat

Somewhere around the 5th grade, our teachers started introducing us to fractions, and many of our schoolmates panicked. Fractions seemed hard. Some of us never got the hang of it, while others breezed through the homework exercises with no problem. Fractions cause problems for computers, too, because there’s no good way to represent fractions in binary notation when you have just two numbers to work with. Or, more accurately, there are too many ways to represent fractions in binary notation. 

Back in the 1950s and ’60s, each computer company made up its own way of doing fractions. Each method was different and incompatible with everybody else’s method. Eventually, the IEEE (Institute of Electrical and Electronic Engineers) stepped in and defined a global, international standard for doing fractions in binary notation. They called it IEEE Standard #754 (IEEE-754 for short), and it’s been the go-to standard for computer hardware and software ever since. Well, almost. 

The problem with doing fractions in binary is that you run out of bits really fast. You can either write really tiny numbers (like the weight of a dust particle) or really huge numbers (like the number of dust particles in the universe), but you can’t do both. We could either come up with one system for big numbers and a different system for small numbers (in addition to the existing system for non-fractions), or we could try to compromise and do both at once. And that’s what the IEEE-754 standard did. 

Really small numbers have a lot of digits to the right of the decimal point, like 0.00000003547, while big numbers have a lot of digits to the left of the decimal point, like 42,683,025,745,118,034.024. It would take a lot of bits to be able to accommodate so many digits on both sides of the decimal point – so we don’t even try. Instead, the IEEE-754 standard lets the decimal point “float” to the left or right depending on the type of the number you’re trying to write. Big numbers push the decimal point to the right so there’s more room for the digits on the left; tiny fractions do the opposite. That’s why everyone calls these “floating-point” numbers. 

Standard Floating-Point

The IEEE-754 standard lays out numbers as shown below. There are always exactly 32 bits, regardless of how big or little the number is. That’s part of the beauty: you always know how much space they’ll take up in memory and how wide your computer’s hardware data paths need to be. Huge numbers and tiny numbers are the same size to a computer.

The IEEE-754 standard floating-point format uses 32 bits (CC BY-SA)

The first bit (on the left, in blue) tells us whether this number is positive or negative. Already, that’s something our normal binary notation couldn’t do. Those numbers started with zero and counted up, but there was no way to write a negative number. Floating-point notation lets us do that.

The next eight bits (in green) are the exponent, which means the number of places to shift the decimal point left or right. This is the “floating” part of floating-point numbers.

Finally, the remaining 23 bits (in pink) are the actual “number” part of the number. (It’s labeled “fraction” in the diagram, but other people call this the mantissa.) In this example, if you wanted to write the number 0.15625, the pink section would hold the 15625 part. The green exponent would tell the computer to shift the decimal point five places to the left to make it 0.15625. Make sense? 

If you wanted to write a big number instead, you’d change the green exponent to indicate you wanted to shift the decimal point to the right, perhaps by six places. Instead of 0.15625 or even 15625.00, you’d get 15,625,000,000. The nifty thing is that all of these numbers (plus a nearly infinite quantity of other numbers) all take up the same 32 bits of space. 

Alas, there are limits to the IEEE-754 format. What if your number (the pink part) doesn’t fit into 23 bits? Too bad. You’ll have to round it down (or round it up; your choice). You’ll also have trouble if the exponent (green part) needs to be bigger than eight bits. The floating-point format isn’t perfect, because real-life numbers are infinite and we’re working with a limited amount of space. Still, it covers most numbers for most cases. 

Enter bfloat16

But there are exceptions; times when IEEE-754 isn’t exactly what you want. Floating-point hardware is notoriously complicated, and computers usually slow way down when they’re doing floating-point math. Like us, they’re better at integers. Once upon a time, an FPU (floating-point unit) was an optional, extra-cost add-on for your computer, precisely because they were so slow and expensive. You didn’t add FP capability if you didn’t really need it. 

Today’s FPUs are cheap, but they’re still slow, especially if you’re doing one floating-point calculation after another, after another, after another. Which pretty much describes machine learning (ML) workloads. ML inference software includes a lot – really a lot – of FP-intensive arithmetic, and it bogs down even the best computer systems. Something needs to change. Either we need to build faster FPUs or we need to simplify the floating-point notation we use. Let’s do both! 

Turns out, most machine learning systems need to handle fractions and/or large numbers, but not with the same kind of accuracy and detail that IEEE-754 provides. That is, we’re willing to trade off precision for speed in ML workloads. IEEE-754 can’t do that – the standard is already written and in widespread use – so we invent a new standard alongside it. Say hello to bfloat16.  

The awkward name stands for “Brain floating-point format with 16 bits,” where Brain was the name of a Google project that spawned the idea. The idea was to cut the data size in half, from 32 bits to 16, thereby making the computer hardware simpler, faster, and cheaper. The tradeoff is that bfloat16 isn’t as accurate as IEEE-754, nor is it as universally accepted.

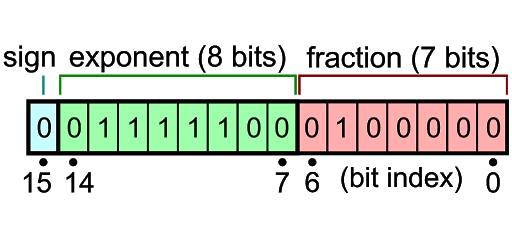
Bfloat16’s condensed floating-point format uses 16 bits (CC BY-SA)

Here’s what a bfloat16 number looks like. At first glance, it’s a lot like the IEEE-754 format we saw above, just shorter. And that’s pretty much true. It still starts off with the positive/negative sign bit (in blue), followed by the eight-bit exponent (in green). Where things differ is in the shortened 7-bit fraction. 

Swapping the earlier 23-bit fraction for just 7 bits means you’ve lost 16 bits from your number. That’s almost two-thirds of the digits you were using before. Imagine writing out a long number (a check to the tax authorities, for example) in just one-third of the space. You might need to leave off some digits if there isn’t enough room. Naturally, you’d start at the left with the most significant digits and fit in as much as you could. If you run out of space, well, at least you got the important part; the rest is details and it’ll just have to be left out. 

Same idea works here. Bfloat16 severely truncates the space for numbers, so you wind up rounding or cutting off some of the less important digits. It’s okay as long as you’re not too worried about exactness or precision. And it is a lot faster because it requires only half the space of a full 32-bit IEEE-754 implementation. 

But wait – doesn’t IEEE-754 already have its own 16-bit format for floating-point numbers? Why don’t we just use that one? Yes, it does, but it’s defined as one sign bit, five exponent bits, and 10 fraction (number) bits. That still adds up to 16 bits, but with way more bits dedicated to the significance of the number and fewer in the exponent. That means it can retain more precision, but with a smaller dynamic range (from largest to smallest numbers). That’s fine for scientific work, but not ideal for ML. 

Since bfloat16 has just as many exponent bits as IEEE-754’s 32-bit format, it can represent numbers just as large and just as small, albeit with occasionally less precision if there are a lot of trailing digits. 

As Google’s engineers point out, the size of an FPU scales with the square of the size of the fractional part (significant number), so reducing that bit field by three bits makes it only one-eighth the size of  an IEEE-754 implementation. That’s a huge win, especially when you’re trying to pack dozens (or maybe hundreds) of them into a single chip. 

More subtly, bfloat16 numbers are easy to convert back and forth from the IEEE-754 standard 32-bit format. Ironically, it’s even easier than converting to/from the “official” 16-bit FP format, because most of the complexity lies in the exponent, not the fraction. That’s useful for as long as bfloat16 remains an upstart fringe standard with spotty support. It also means it’s easy to exchange data with other machines that adhere to the IEEE-754 format. 

Paradoxically, some neural nets are actually more accurate with bfloat16’s reduced precision than they are with more accurate 32-bit FP numbers. So, there’s little incentive to stick with the IEEE-754 standard, especially when the hardware size, cost, and performance improvements are factored in. The only drawback is that bfloat16 hardware isn’t very common – yet. 

Just about every ML startup builds bfloat16-compatible FPUs into their chips now. Even Intel has started adding bfloat16 capability to a few of its x86 processors. It’s going to be pretty much mandatory from this point on, so making friends with bfloat16 now will pay off down the road, for you and for the machine.